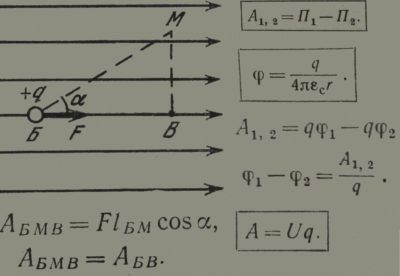Содержание
Энергия заряженного конденсатора – это работа, потраченная на его зарядку.
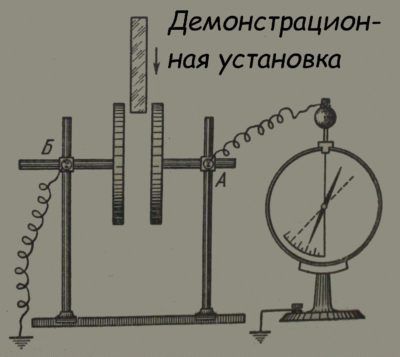
Из истории
Первым конденсатором считается лейденская банка. Её разработали независимо сразу двое учёных:
- Эвальд Георг фон Клейст (11 октября 1745 года).
- Питер ван Мушенбрук (1745 – 1746 годы).
Двумя десятилетиями позже на свет появился электрофорус (1762 год), рассматриваемый как первый плоский конденсатор. Тогда не существовало терминов, вопросы накопления заряда мало интересовали. Учёные пока что развлекались получением статического заряда. К примеру, ван Мушенбрук испытывал лейденскую банку на слишком смелых студентах, когда сам оказался однажды полупарализован электрическим зарядом.
Наука не шла вперёд, хотя светила, включая Бенджамина Франклина, вовсю толкали паровоз. Современный этап развития физики начался с Алессандро Вольта. Учёный оказался привлечён конструкцией электрофоруса и заинтригован. Натёртая резина могла сколь угодно долго заряжать металлическую пластину. В то время предполагалось, что электричество переносится флюидами атмосферы, и Вольта считал аналогично. Узрев, что электрофорус способен запасать заряд, учёный решил посчитать и количество.
Концепция Вольты
Как свидетельствуют записки учёного, уже в 1778 году он получил представление о разнице потенциалов, которые называл tension – напряжение. С 1775 года Вольта придерживается концепции электрической ёмкости – capacita, выдвинутой его учителем Беккарией. Вольта уже знает, что электрофорус способен накопить заряд, называет прибор конденсатором, и решает подтвердить теорию практикой. Иначе – найти взаимосвязь напряжения, ёмкости и объёмом (quantita) заряда.
Вольта начал с лейденской банки. Он заряжал её от статического генератора и пробовал определить энергию конденсатора тремя путями:
- Наблюдал получаемую искру электрической дуги от различной конструкции лейденских банок, заряженных одинаковым напряжением.
- Измерял количество произведённой электростатическими генераторами трения работу, пока показания электрометра не росли до определённого уровня.
- Разряжал лейденские банки на открытом воздухе и пытался сравнить производимый ими электрический шок по истечении времени.
Все перечисленное привело исследователя к странным выводам, что высокие лейденские банки более вместительные (при одинаковых площадях обкладок и прочих равных условиях). Вероятно, это связано со скоростью разряда их дуги на воздухе вследствие различий в кривизне поверхностей. Силу разряда Вольта увязывал с электрическим током: чем быстрее течёт флюид, тем более жаркий (по ощущениям) эффект. В результате, Вольта счёл, что разница потенциалов единственная определяет процесс возникновения удара. Он решил, что напряжение допустимо измерить двумя путями:
- Через количество оборотов генератора статического заряда.
- Сравнивая силу электрического удара при разряде лейденской банки.
Вольта нашёл, что заряжая пустую лейденскую банку от полной, шок получается вдвое слабее. Постепенно (1782 год) Вольта пришёл к выводу, что вышеуказанные величины соотносятся между собой: tension x capacity ~ load, в современном мире выглядит как U C = q или C = q / U.
Вольта заключил, что ёмкость больше там, где при меньшем напряжении вмещается больше заряда. Последовало заключение, что количество накопленного флюида прямо пропорционально площади обкладок плоского конденсатора. Что согласуется с современными формулами. Вольта обобщил знания на случай произвольного проводника (экспериментировал со стержнями лейденских банок). Изменяя расстояние между обкладками, установил:
С ~ S / d.
Что фактически стало выражением ёмкости плоского конденсатора. Вольта объяснил зависимость наличием некоего сопротивления (resistance) между обкладками, подразумевая воздух. Изменяя дистанцию, удаётся варьировать этот параметр в обе стороны. Это слегка не согласуется с современными концепциями, но Вольта помог Георгу Ому 40 лет спустя вывести зависимость между током и напряжением.
Фактически измерения проделывались на основе работы поля, проявлявшейся лишь вследствие заряда конденсатора. Очевидно, что указанная величина равна энергии – одной из первых физических характеристики, использованных для вывода аналитических выражений.
Единицы измерения
Энергию и работу принято измерять в джоулях, электрическое напряжение и потенциал – в вольтах.
Вольтом называется разница потенциалов, при перемещении единичного положительного заряда между которыми совершается работа в 1 джоуль.
Ёмкость конденсатора
Выше показано, как выразил ёмкость конденсатора Вольта. Формула понадобится при вычислении энергии. Направление силовых линий определено Кулоном, согласно показаниям крутильных весов, что позволило физикам со временем вывести собственные формулы. Вольта оказался близок к внедрению понятия электрического потенциала, нельзя обделить упоминанием его наставников: Беккария и Кавендиша. Благодаря упомянутым людям физика стала пристально присматриваться к магнетизму и электричеству.
Работа электрического поля
Электрическое поле называется потенциальным. Это значит, что работа его сил не зависит от траектории движения заряда, исключительно от энергии начального и конечного положения. Напомним, согласно определению:
Электрическое поле – это материя, посредством которой взаимодействуют электрические заряды.
Электрическое поле воздействует исключительно на электрические заряды. Создаётся двумя путями:
- Электрическими зарядами. Силовые линии начинаются на положительных и заканчиваются на отрицательных зарядах.
- Изменяющимся магнитным полем. При этом образуется электромагнитная волна, что используется в генераторах.
Когда говорят, что излучение приборов действует на человека, подразумеваются и магнитная, и электрическая составляющие. Особенно опасна первая, которая с большим трудом экранируется. Электрическое поле, рассматриваемое в физике школьного курса, считается стационарным, а линии напряжённости его параллельны. Приводятся два примера:
- Допустим, заряд перемещается вдоль линий поля на некоторое расстояние l. Тогда работа находится по упрощённой формуле A = Fl, где F – сила, действующая на заряд.
- Теперь предположим, что заряд переместился из прежней точки по косой линии. Так, что проекция пути lb на силовые линии снова равна l. Участок прямолинейный, угол отклонения – В. Работа вычисляется по формуле с учётом геометрических соотношений как A = FlbcosB = Fl.
Этот простой случай, легко распространяется на любую форму линий напряжённости. Сие означает, что в электрическом поле работа не зависит от траектории, а значит, равна разнице потенциалов поля: А = П1 – П2. Формула применима для любого поля. Чтобы адаптировать выражение, вводят понятие электрического потенциала как энергию единичного положительного заряда – ф = П / q1. Тогда формула для работы принимает иной вид.
Электрическим напряжением между двумя точками называется разница потенциалов между ними. Умножая указанное значение на величину заряда, поскольку величина удельная, получаем: А = (ф1 – ф2) q = U q. Потенциал через величины поля находится:
ф = q / 4 ε Пи r,
где q – величина заряда, создающего поля; ε – диэлектрическая проницаемость среды (для воздуха и вакуума равна единице); Пи = 3,14; r – расстояние до исследуемой точки от упомянутого заряда. Формула годится далеко не для любых случаев, приведена для примера. Допустимо применять для заряда, распределённого по поверхности шара, и точек, лежащих вне указанной поверхности.
Напряжённость поля плоского конденсатора
В физике рассмотрение всегда ведётся на примере плоского конденсатора, это простейший случай. Поле плоского конденсатора в точности соответствует описанному выше.
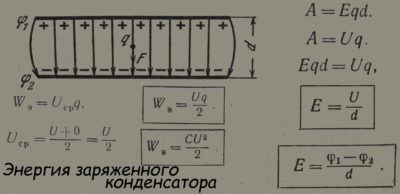
Пусть на обкладках присутствует некий заряд. Очевидно, что объем его одинаков, а знаки различны. Работа по перемещению заряда между обкладками равна A = F d, где под d понимается ширина зазора. Формула прямиком приводит к связи с напряжённостью: А = Е q d = U q (см. выше). Следовательно, запишем, что Е = U / d.
Напряжённость поля показывает силу, с которой действует на единичный точечный заряд.
Энергия заряженного конденсатора
Теперь подумаем, как посчитать энергию при заряде конденсатора. Потребуется вспомнить формулу потенциала, создаваемого точечным зарядом. Видно, что он убывает линейно расстоянием. Но в рассматриваемом случае первый заряд положительный и находится на одной обкладке, а второй отрицательный и расположился напротив. Следовательно, по мере движения в направлении силовой линии отмечается такая картина:
- Потенциал положительного заряда падает.
- Потенциала отрицательного заряда растёт.
Причём скорость изменения их одинакова. Следовательно, между обкладками плоского конденсатора потенциал поля не меняется. Теперь вспомним, от чего он зависит. В изучаемом случае величины постоянны, кроме заряда, накопленного на обкладках после подачи напряжения. Значит, потенциал постепенно растёт и линейно зависит от заряда, причём уже не важен график собственно процесса. Получается прямая линия.
Это значит, что в начальный момент времени потенциал равен нулю, потом растёт до определённого предела. Графиком зависимости потенциала от количества зарядов станет прямая линия (по времени выходит экспонента). Теперь поясним, зачем производились умозаключения:
- Известно, что энергия выражается затраченной работой.
- Значит, допустимо записать формулу W = U q. Выглядит просто, ведь заряд связан с ёмкостью, но чему равно напряжение? Следует напомнить, что на конденсаторе оно растёт по экспоненте в процессе заряда. Брать интеграл по времени? Физики уже решили задачу.
- Потенциал (напряжение) линейно зависит от заряда, заключаем, что общая работа находится усреднением, что при прямой линии сводится к операции деления на 2.
В итоге: W = U q / 2. Теперь подставим сюда выражение, полученное Алессандро Вольта, и выйдет: W = C U2 / 2. Полученным выражением и пользуются при расчётах.
https://youtu.be/4HPhCLOwAAs
Мера энергии заряженного конденсатора
При расчёте фильтров цепей питания и прочих электрических фильтров встаёт задача определения номиналов. Кажется, достаточно взять формулу частоты резонансного контура, но простота обманчива. Легко убедиться, что одинаковому ответу соответствует множество значений. Которое выбрать?
Чем больше мощность источника, питания прибора, тем большая энергия здесь проходит в единицу времени. Для конденсатора она зависит от квадрата напряжения и ёмкости, для дросселя – от величины электрического тока и индуктивности. Узнав период единственного колебания, эту цифру легко привязать к мощности, как выполняемой работе в единицу времени.
В результате инженер сумеет сказать приблизительно, какого размера ёмкость требуется в конкретном случае. Расчёт ведётся изначально по энергии заряженного конденсатора.
Аналогичное происходит в любой цепи. Конденсаторы служат для фильтрации и гальванической развязки, обязаны легко пропускать нужную частоту и оставаться ёмкими, чтобы не стать бутылочным горлышком в системе.