Содержание
Правило буравчика – упрощенная наглядная демонстрация при помощи одной руки правильного умножения двух векторов. Геометрия школьного курса подразумевает осведомленность учеников о скалярном произведении. В физике часто встречается векторное.
Понятие вектора
Полагаем, нет смысла истолковывать правило буравчика при отсутствии знания определения вектора. Требуется открыть бутылку – знание о правильных действиях поможет. Вектором называют математическую абстракцию, не существующую реально, выказывающую указанные признаки:
- Направленный отрезок, обозначаемый стрелкой.
- Точкой начала послужит точка действия силы, описываемой вектором.
- Длина вектора равна модулю силы, поля, прочих описываемых величин.
Не всегда затрагивают силу. Векторами описывается поле. Простейший пример показывают школьникам преподаватели физики. Подразумеваем линии напряженности магнитного поля. Вдоль обычно рисуются векторы по касательной. В иллюстрациях действия на проводник с током увидите прямые линии.
Векторные величины часто лишены места приложения, центры действия выбираются по договоренности. Момент силы исходит из оси плеча. Требуется для упрощения сложения. Допустим, на рычаги различной длины действуют неодинаковые силы, приложенные к плечам с общей осью. Простым сложением, вычитанием моментов найдем результат.
Векторы помогают решить многие обыденные задачи и, хотя выступают математическими абстракциями, действуют реально. На основе ряда закономерностей возможно вести предсказание будущего поведения объекта наравне со скалярными величинами: поголовье популяции, температура окружающей среды. Экологов интересуют направления, скорость перелета птиц. Перемещение является векторной величиной.
Правило буравчика помогает найти векторное произведение векторов. Это не тавтология. Просто результатом действия окажется тоже вектор. Правило буравчика описывает направление, куда станет указывать стрелка. Что касается модуля, нужно применять формулы. Правило буравчика – упрощенная чисто качественная абстракция сложной математической операции.
Аналитическая геометрия в пространстве
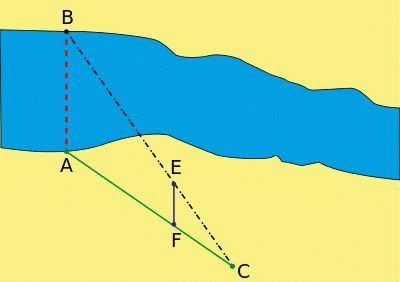
Каждому известна задачка: стоя на одном берегу реки, определить ширину русла. Кажется уму непостижимым, решается в два счета методами простейшей геометрии, которую изучают школьники. Проделаем ряд несложных действий:
- Засечь на противоположном берегу видный ориентир, воображаемую точку: ствол дерева, устье ручейка, впадающего в поток.
- Под прямым углом линии противоположного берега сделать засечку на этой стороне русла.
- Найти место, с которого ориентир виден под углом 45 градусов к берегу.
- Ширина реки равна удалению конечной точки от засечки.
Используем тангенс угла. Не обязательно равен 45 градусов. Нужна большая точность – угол лучше брать острым. Просто тангенс 45 градусов равен единице, решение задачки упрощается.
Аналогичным образом удается найти ответы на животрепещущие вопросы. Даже в микромире, управляемом электронами. Можно однозначно сказать одно: непосвященному правило буравчика, векторное произведение векторов представляются скучными, занудными. Удобный инструмент, помогающий в понимании многих процессов. Большинству будет интересным принцип работы электрического двигателя (безотносительно к конструкции). Легко может быть объяснен использованием правила левой руки.
Во многих отраслях науке бок-о-бок идут два правила: левой, правой руки. Векторное произведение иногда может описываться так или эдак. Звучит расплывчато, предлагаем немедленно рассмотреть пример:
- Допустим, движется электрон. Отрицательно заряженная частица бороздит постоянное магнитное поле. Очевидно, траектория окажется изогнута благодаря силе Лоренца. скептики возразят, по утверждениям некоторых ученых электрон не частица, а скорее, суперпозиция полей. Но принцип неопределенности Гейзенберга рассмотрим в другой раз. Итак, электрон движется:
Расположив правую руку, чтобы вектор магнитного поля перпендикулярно входил в ладонь, вытянутые персты указывали направление полета частицы, отогнутый на 90 градусов в сторону большой палец вытянется в направлении действия силы. Правило правой руки, являющееся иным выражением правила буравчика. Слова-синонимы. Звучит по-разному, по сути – одно.
- Приведем фразу Википедии, отдающую странностью. При отражении в зеркале правая тройка векторов становится левой, тогда нужно применять правило левой руки вместо правой. Летел электрон в одну сторону, по методикам, принятым в физике, ток движется в противоположном направлении. Словно отразился в зеркале, поэтому сила Лоренца определяется уже правилом левой руки:
Если расположить левую руку, чтобы вектор магнитного поля перпендикулярно входил в ладонь, вытянутые персты указывали направление течения электрического тока, отогнутый на 90 градусов в сторону большой палец вытянется, указывая вектор действия силы.
Видите, ситуации похожие, правила просты. Как запомнить, которое применять? Главный принцип неопределенности физики. Векторное произведение вычисляется во многих случаях, причем правило применяется одно.
Какое правило применить
Слова синонимы: рука, винт, буравчик
Вначале разберем слова-синонимы, многие начали спрашивать себя: если тут повествование должно затрагивать буравчик, почему текст постоянно касается рук. Введем понятие правой тройки, правой системы координат. Итого, 5 слов-синонимов.
Потребовалось выяснить векторное произведение векторов, оказалось: в школе это не проходят. Проясним ситуацию любознательным школьникам.
Школьные графики на доске рисуют в декартовой системе координат Х-Y. Горизонтальная ось (положительная часть) направлена вправо – надеемся, вертикальная – указывает вверх. Делаем один шаг, получая правую тройку. Представьте: из начала отсчета в класс смотрит ось Z. Теперь школьники знают определение правой тройки векторов.
В Википедии написано: допустимо брать левые тройки, правые, вычисляя векторное произведение, несогласны. Усманов в этом плане категоричен. С разрешения Александра Евгеньевича приведем точное определение: векторным произведением векторов называют вектор, удовлетворяющий трем условиям:
- Модуль произведения равен произведению модулей исходных векторов на синус угла меж ними.
- Вектор результата перпендикулярен исходным (вдвоем образуют плоскость).
- Тройка векторов (по порядку упоминания контекстом) правая.
Правую тройку знаем. Итак, если ось Х – первый вектор, Y – второй, Z будет результатом. Почему назвали правой тройкой? По-видимому, связано с винтами, буравчиками. Если закручивать воображаемый буравчик по кратчайшей траектории первый вектор-второй вектор, поступательное движение оси режущего инструмента станет происходить в направлении результирующего вектора:
- Правило буравчика применяется к произведению двух векторов.
- Правило буравчика качественно указывает направление результирующего вектора этого действия. Количественно длина находится выражением, упомянутым (произведение модулей векторов на синус угла меж ними).
Теперь каждому понятно: сила Лоренца находится согласно правилу буравчика с левосторонней резьбой. Векторы собраны левой тройкой, если взаимно ортогональны (перпендикулярны один другому), образуется левая система координат. На доске ось Z смотрела бы в направлении взгляда (от аудитории за стену).
Простые приемы запоминания правил буравчика
Люди забывают, что силу Лоренца проще определять правилом буравчика с левосторонней резьбой. Желающий понять принцип действия электрического двигателя должен как дважды два щелкать подобные орешки. В зависимости от конструкции число катушек ротора бывает значительным, либо схема вырождается, становясь беличьей клеткой. Ищущим знания помогает правило Лоренца, описывающее магнитное поле, где движутся медные проводники.
Для запоминания представим физику процесса. Допустим, движется электрон в поле. Применяется правило правой руки для нахождения направления действия силы. Доказано: частица несет отрицательный заряд. Направление действия силы на проводник находится правилом левой руки, вспоминаем: физики совершенно с левых ресурсов взяли, что электрический ток течет в направлении противоположном тому, куда направились электроны. И это неправильно. Поэтому приходится применять правило левой руки.
Не всегда следует идти такими дебрями. Казалось бы, правила больше запутывают, не совсем так. Правило правой руки часто применяется для вычисления угловой скорости, которая является геометрическим произведением ускорения на радиус: V = ω х r. Многим поможет визуальная память:
- Вектор радиуса круговой траектории направлен из центра к окружности.
- Если вектор ускорения направлен вверх, тело движется против часовой стрелки.
https://www.youtube.com/watch?v=enwbrdUcbvU
Посмотрите, здесь опять действует правило правой руки: если расположить ладонь так, чтобы вектор ускорения входил перпендикулярно в ладонь, персты вытянуть по направлению радиуса, отогнутый на 90 градусов большой палец укажет направление движения объекта. Достаточно однажды нарисовать на бумаге, запомнив минимум на половину жизни. Картинка действительно простая. Больше на уроке физики не придется ломать голову над простым вопросом – направление вектора углового ускорения.
Аналогичным образом определяется момент силы. Исходит перпендикулярно из оси плеча, совпадает направлением с угловым ускорением на рисунке, описанном выше. Многие спросят: зачем нужно? Почему момент силы не скалярная величина? Зачем направление? В сложных системах непросто проследить взаимодействия. Если много осей, сил, помогает векторное сложение моментов. Можно значительно упростить вычисления.