Когерентные волны

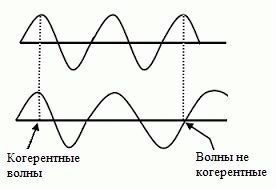
Когерентные волны – это колебания с постоянной разностью фаз. Разумеется, условие выполняется не в каждой точке пространства, лишь на отдельных участках. Очевидно, что для удовлетворения определению частоты колебаний также предвидятся равными. Прочие волны бывают когерентны лишь на некотором участке пространства, а дальше разность фаз меняется, и это определение использовать уже нельзя.

Обоснование применения

Когерентные волны считаются упрощением, не встречающимся на практике. Математическая абстракция помогает во многих отраслях науки: космос, термоядерные и астрофизические исследования, акустика, музыка, электроника и, конечно, оптика.

Для реальных приложений применяются упрощённые методы, в числе последних трёхволновая система, основы применимости кратко изложены ниже. Для анализа взаимодействия возможно задать, к примеру, гидродинамическую или кинетическую модель.

Интерференция волн

Решение уравнений для когерентных волн позволяет предсказать устойчивость систем, функционирующих с использованием плазмы. Теоретический подсчёт показывает, что иногда амплитуда результата за короткое время растёт бесконечно. Что означает создание взрывоопасной ситуации. Решая уравнения для когерентных волн, подбором условий удаётся избежать неприятных последствий.

Определения

Вначале введём ряд определений:

• Монохроматической называется волна единственной частоты. Ширина её спектра равна нулю. На графике это единственная гармоника.
• Спектр сигнала – графическое представление амплитуды слагающих гармоник, где по оси абсцисс (ось Х, горизонтальная) откладывается частота. Спектром синусоидального колебания (монохроматической волны) становится единственная спектринка (вертикальная чёрточка).
• Преобразованиями Фурье (обратным и прямым) называют разложение сложного колебания на монохроматические гармоники и обратное сложение целого из разрозненных спектринок.
• Волновой анализ цепей для сложных сигналов не проводится. Вместо этого происходит разложение на отдельные синусоидальные (монохроматические) гармоники, для каждой сравнительно просто составить формулы описания поведения. При расчёте на ЭВМ этого хватает для анализа любых ситуаций.
• Спектр любого непериодического сигнала бесконечен. Границы его обрезаются до разумных пределов перед проведением анализа.
• Дифракцией называется отклонение луча (волны) от прямолинейной траектории вследствие взаимодействия со средой распространения. К примеру, проявляется при преодолении фронтом щели в препятствии.
• Интерференцией называется явление сложения волн. Из-за чего наблюдается весьма причудливая картина из чередующихся полос света и тени.
• Рефракцией называется преломление хода волны на разделе двух сред с различными параметрами.

Волны колебаний

Понятие когерентности

Советская энциклопедия говорит, что волны одинаковой частоты неизменно когерентны. Это верно исключительно для отдельно взятых неподвижных точек пространства. Фаза определяет результат сложения колебаний. К примеру, противофазные волны одной амплитуды дают прямую линию. Такие колебания гасят друг друга. Самая большая амплитуда у синфазных волн (разность фаз равна нулю). На этом факте основан принцип действия лазеров, зеркальная и фокусирующая система пучков света, особенности получения излучения делают возможной передачу информации на колоссальные расстояния.

Согласно теории взаимодействия колебаний когерентные волны образуют интерференционную картину. У новичка возникает вопрос: свет лампочки не кажется полосатым. По простой причине, что излучение не одной частоты, а лежит в пределах отрезка спектра. И участок, причём, приличной ширины. Из-за неоднородности частот волны беспорядочные, не проявляют свои теоретически и экспериментально в лабораториях обоснованные и доказанные свойства.

Хорошей когерентностью обладает луч лазера. Его используют для связи на дальние расстояния при прямой видимости и прочих целей. Когерентные волны дальше распространяются в пространстве и на приёмнике подкрепляют друг друга. В пучке света разрозненной частоты эффекты способны вычитаться. Возможно подобрать условия, что излучение исходит от источника, но на приёмнике не зарегистрируется.

Обычный свет лампочки тоже работает не на полную мощность. Достичь КПД в 100% на современном этапе развития техники не представляется возможным. К примеру, газоразрядные лампы страдают сильной дисперсией частот. Что касается светодиодов, основатели концепции нанотехнологий обещали создать элементную базу для производства полупроводниковых лазеров, но напрасно. Значительная часть разработок засекречена и рядовому обывателю недоступна.

Лишь когерентные волны проявляют волновые качества. Действуют согласованно, как лучинки веника: по одной легко сломать, вместе взятые – выметают мусор. Волновые свойства – дифракция, интерференция и рефракция – характерны для всех колебаний. Просто зарегистрировать эффект сложнее из-за беспорядочности процесса.

Когерентные волны не демонстрируют дисперсии. Показывают одну частоту и одинаково отклоняются призмой. Все примеры волновых процессов в физике даются, как правило, для когерентных колебаний. На практике приходится учитывать присутствующую малую ширину спектра. Что накладывает особенности на процесс расчёта. Как зависит реальный результат от относительной когерентности волны – пытаются ответить многочисленные учебники и разрозненные издания с замысловатыми названиями! Единого ответа не существует, он сильно зависит от отдельно взятой ситуации.

Волновые пакеты

Для облегчения решения практической задачи можно ввести, к примеру, определение волнового пакета. Каждый из них разбивается дальше на мелкие части. И эти подразделы взаимодействуют когерентно между аналогичными частотами другого пакета. Подобный аналитический метод широко распространён в радиотехнике и электронике. В частности, понятие спектра изначально вводилось для того, чтобы дать в руки инженеров надёжный инструмент, позволяющий оценить поведение сложного сигнала в конкретных случаях. Оценивается малая толика воздействия каждого гармонического колебания на систему, потом конечный эффект находится их полным сложением.

Следовательно, при оценке реальных процессов, не являющихся даже близко когерентными, допустимо разбить объект анализа на простейшие составляющие, чтобы оценить результат процесса. Расчёт упрощается с применением вычислительной техники. Машинные эксперименты показывают достоверность формул для имеющейся ситуации.

На начальном этапе анализа полагают, что пакеты с малой шириной спектра возможно условно заменить гармоническими колебаниями и в дальнейшем пользоваться обратным и прямым преобразованием Фурье для оценки результата. Эксперименты показали, что разброс фаз между выбранными пакетами постепенно возрастает (колеблется с постепенным увеличением разброса). Но для трёх волн разница постепенно сглаживается, согласуясь с излагаемой теорией. Накладывается ряд ограничений:

1. Пространство должно быть бесконечным и однородным (k-пространство).
2. Амплитуда волны не затухает с увеличением дальности, но меняется с течением времени.

Доказано, что в такой среде каждой волне удаётся подобрать конечный спектр, что автоматически делает возможным машинный анализ, а при взаимодействии пакетов спектр результирующей волны уширяется. Колебания по сути когерентными не считаются, но описываются уравнением суперпозиции, представленном ниже. Где волновой вектор ω(k) определяется по дисперсионному уравнению; Еk признано амплитудой гармоники рассматриваемого пакета; k – волновое число; r – пространственная координата, для показателя решается представленное уравнение; t – время.

Уравнение суперпозиции

Время когерентности

В реальной ситуации разнородные пакеты когерентны лишь на отдельном интервале. А далее расхождение фаз становится слишком большим, чтобы применять описанное выше уравнение. Чтобы вывести условия возможности вычислений, вводится понятие времени когерентности.

Полагается, что в начальный момент фазы всех пакетов одинаковы. Выбранные элементарные доли волны когерентны. Тогда искомое время находится как отношение числа Пи к ширине спектра пакета. Если время превысило когерентное, в данном участке уже нельзя использовать формулу суперпозиции для сложения колебаний – фазы слишком сильно отличаются друг от друга. Волна уже не когерентна.

Пакет возможно рассматривать, словно он характеризуется случайной фазой. В этом случае взаимодействие волн идёт по отличающейся схеме. Тогда находятся фурье-компоненты по указанной формуле для дальнейших расчётов. Причём взятые для расчёта две прочие компоненты берутся из трёх пакетов. Это случай совпадения с теорией, упомянутый выше. Следовательно, уравнение показывает зависимость всех пакетов. Точнее – результата сложения.

Для получения наилучшего результата нужно, чтобы ширина спектра пакета не превышала числа Пи, делённого на время решения задачи суперпозиции когерентных волн. При расстройке частоты амплитуды гармоник начинают осциллировать, точный результат получить сложно. И наоборот, для двух когерентных колебаний формула сложения упрощается максимально. Амплитуда находится как квадратный корень из суммы исходных гармоник, возведённых в квадрат и сложенных с собственным удвоенным произведением, помноженным на косинус разности фаз. У когерентных величин угол равен нулю, результат, как уже указано выше, получается максимальным.

Наравне с временем и длиной когерентности используют термин «длина цуга», что является аналогом второго термина. Для солнечного света эта дистанция составляет один микрон. Спектр нашего светила крайне широкий, что объясняет настолько мизерную дистанцию, где излучение считается когерентным самому себе. Для сравнения, длина цуга газового разряда достигает 10 см (в 100000 раз больше), а у лазера излучение сохраняет свойства и на километровых расстояниях.

С радиоволнами намного проще. Кварцевые резонаторы позволяют достичь высокой когерентности волны, чем объясняются пятна уверенного приёма на местности, граничащие с зонами молчания. Аналогичное проявляется при изменении имеющейся картины с течением суток, движением облаков и прочими факторами. Изменяются условия распространения когерентной волны, и интерференционная суперпозиция оказывает влияние в полной мере. В радиодиапазоне на низких частотах длина когерентности может превышать поперечник Солнечной системы.

Условия сложения сильно зависят от формы фронта. Наиболее просто задача решается для плоской волны. В действительности фронт обычно является сферическим. Точки синфазности находятся на поверхности шара. В бесконечно удалённой от источника местности условие плоскости возможно принять за аксиому, и дальнейший расчёт вести согласно взятому постулату. Чем ниже частота, тем проще создать условия для выполнения расчёта. И наоборот, источники света со сферическим фронтом (вспомним Солнце) сложно подогнать под стройную теорию, написанную в учебниках.